Batch 2 - Class 101 - Paper Sizes
Pre-Class Problem:
- (Geoffrey: 113) One of the following integers, and only one, is a square. Can you find out which one? (Hint: Use Digital Roots)
3,669,517,136,205,224
1,898,732,825,398,318
4,751,006,864,295,101
5,901,643,220,186,100
7,538,062,944,751,882
2,512,339,789,576,516
- Answer: The unit digit of a square has to be 1,4,5,6,9,0 so it eliminates 2nd and 5th numbers. The digital root of a square is 1,4,7,9 - this leaves only the 6th number
Attendance: Tishyaa, Khushi, Muskaan, Anishka, Arnav, Anshi
Class Notes:
Area Shock
Its my birthday this month and I am going to bake a triangular cake. Show how I can cut and take out a piece of cake, divide the remainder of the cake into six pieces, rearrange them, and repeat! I am set for an infinite supply of cake!
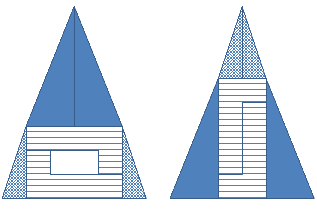
Whats going on?
- Answer: The slope of two triangles is not exactly the same. So there is a slight bulge in first one and slight contraction on second one. That is what creates the illusion of the area mismatch.
The A4 Paper
The A series of international paper sizes sets A4 paper as 297mm by 210 mm (which is approximately 11 ¾ inches by 8 ¼ inches). Why the numbers 297 and 210?
The A series of international paper sizes follows two criteria: the paper size must be pleasant to handle and pleasant to look at, and when the paper is folded in half, one should obtain a smaller rectangle of paper of the same proportions as the original.
What size rectangular paper meets these criteria?
The second criterion is a mathematical one, so let’s look at that one first. We want a rectangle of some proportions so that half that rectangle has the same proportions. Suppose we start with a rectangle a units on the long side and b units on the short side. Then its long-to-short proportions are a/b .
If we fold the rectangle in half, now the sides are b and a/2, so the ratio is 2b/a, which must be the same proportion as original paper. Solving for this, a/b=SQRT(2). Since SQRT(2) is irrational, there are no numbers a and b, that would satisfy this criteria! So while A4 paper size 297 x 210 is pleasant, it is not equal to SQRT(2). That ratio is 297/210 = 99/70. Why?
.png)
Scholars since the time of antiquity have been thinking about and playing with the number the square root of two. Theon of Smyrna (ca 140 CE), for example, was fully aware that if a rectangle of sides a units and b units, has proportions that approximate SQRT(2) , then drawing a square on the small side of that rectangle followed by another square on the long side of what results gives a new, larger rectangle with proportions that more closely approximate 2 . That is, if a b approximates SQRT(2) , then (a+2 b)/(a+b) is a better approximation.
.png)
What happens if we start with a square of size 1x1 and keep expanding? What are the successive rectangles and do they give better approximations of SQRT(2)? Check. What number do you reach if you keep building the sequence? 1/1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169: Watch out - there is out 99/70!
All the remaining standard A paper sizes, A1, A2, A3, and so on, are close approximations to scaled versions of this A4 size.They (almost) fit together to make their own tiling pattern.
.png)
What will happen if you start with 1x1, and keep adding just one square at a time along the longer edge?
- We get our fibonacci sequence and the golden ratio of 1.618...
Centering a Circle
Using nothing more than an A4 paper and a pencil, mark the center of a circle very accurately!
Instructor Notes: Let kids try and formulate approaches to this.
Side Exercise: Suppose we have two points on a surface, and a rectangular paper is pushed through the gap between points, till it touches the two points on edges. Mark the point of the vertex.
.png)
If you pushed the paper to the two points at another angle, you would get another point. If you did this many times, and joined all the blue points, what shape will you get?
Instructor Notes: Kids are likely to come to a visual conclusion that its a circle - can you prove it?
What do you need to prove to prove that its a circle? That the blue point is the same distance from center of black dots, as the center is from each of the dots. How do you do that? Give kids time after drawing this diagram... If they dont get it for few minutes, draw an inverted shape and ask them to think about it.
.png)
.png)
Being two diagonals of rectangle bisecting each other, all four segments have to be the same!
Lets come back to the original problem... If we know that paper pushing leads to circular segments, how do we determine the center of an arbitrary circle accurately?
What if the paper you were pushing was not right angled? What kind of a shape would it trace then?
.png)
Homework
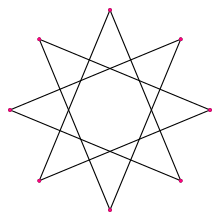
- (Geoffrey: 28) There is an eight pointed star. You must place a penny on one point, and slide it along the line till it reaches another point across. Place seven pennies in this manner.
References:
Mathematical Puzzles, Geoffrey Mott-Smith